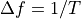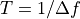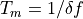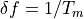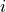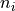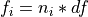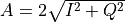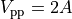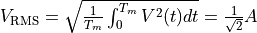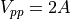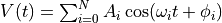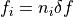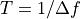Glossary

Multi-frequency lockin measurement and intermodulation spectroscopy are developing fields and the language used to describe the concepts changes as our understanding becomes more refined. Mathematical and programing symbols are part of this language. We provide this glossary to establish definitions of the terms used in this manual.

Table of symbols used in this manual

Term

Programming

Math

Base tone

Df = 1/T

\Delta f = 1/T

Waveform period

T = 1/Df

T = 1/\Delta f

Measurement time

Tm = 1/df

T_m = 1 / \delta f

Measurement bandwidth

df = 1/Tm

\delta f = 1 / T_m

Tone index

idx

i

Tone-integer array

narray

n_i

Frequency array

freqs = narray*df

f_i = n_i * df

amplitude

The word amplitude is used in different ways and its exact definition depends on the context. Consider a signal consisting of one pure tone.

V(t) = A \cos(\omega t + \phi).

For this single-frequency signal, the amplitude A is just the peak value of the signal. This amplitude is related to the two quadratures I and Q by the following expression,

A = 2 \sqrt{I^2 + Q^2}

as described in the section on lockin measurement. We may also refer to the peak-to-peak amplitude of the signal,

V_\mathrm{pp} = 2A

or the root-mean-square (rms) amplitude of the signal,

V_\mathrm{RMS} = \sqrt{ \frac{1}{T_m}\int_0^{T_m} V^2(t) dt} = \frac{1}{\sqrt{2}}A

when the measurement time window T_m is an integer multiple of the period T=2\pi /\omega.

The table below summarizes how these various amplitudes are related.

Name

Symbol

Mathematical relationship

amplitude

A

A

quadrature amplitude

Aquad

\sqrt{I^2 + Q^2} = A/2 *

peak-to-peak amplitude

Vpp

V_{pp} = 2A

root-mean-square amplitude

Vrms

V_{rms}=\tfrac{1}{\sqrt{2}}A *

* =A at \omega=0 or DC

Note that when we build a multifrequency waveform consisting of a superposition (sum) of N sinusoidal oscillations,

V(t) = \sum_{i=0}^N{A_i \cos(\omega_i t + \phi_i)}

it is not trivial to determine the peak, or maximum voltage of the signal. Each component oscillates with a different frequency and arbitrary phase and one can not generally say how all signals superpose to create the resultant signal.

base tone

The frequency of the base tone is the inverse of the waveform period. Any periodic waveform is represented on a comb in the frequency-domain, where all tones in the comb have frequencies that are integer multiples of the frequency of the base tone. The base tone is the greatest common divisor of all frequencies in the comb.

programing symbol - Df = 1/T

math symbol \Delta f = 1/T

frequency comb

We use frequency comb to mean any superposition of sine and cosine oscillations from a discrete set frequencies which are integer multiples of a base tone \Delta f.

f_i = k_i \Delta f,

where k_i are a set of integers.

The term ‘comb’ is used because the spectrum of all such tones with equal amplitude, looks like the instrument used to straighten your hair. The Fourier components of a comb are referred to as tones.

In optics, frequency combs generated from nonlinear media often have an offset frequency.

f_i = f_\mathrm{offset} + k_i \Delta f

The MLA™ digitally synthesis a comb having a maximum of 40 tones, with f_\mathrm{offset}=0, and measures the response these frequencies.

measurement time window

The time window over which Fourier sums, or Lockin calculations are preformed. For optimal Fourier analysis, all tones of a multifrequency waveform should have a period which is an integer fraction of the measurement time window. The measurement time is the inverse of the measurement bandwidth.

programing symbol: - Tm = 1/df

math symbol T_m = 1 / \delta f

measurement bandwidth

The inverse of the time window. Noise power is inversely proportional to the measurement bandwidth.

programing symbol - df = 1/Tm

math symbol \delta f = 1 / T_m

Do not use and depreciate: delta_f, Delta_f, \Delta f

pixel

A fundamental unit of multifrequency lockin data containing the quadrature amplitudes at all measured frequencies. Pixel can also refer to the particular measurement time window on which this lockin data was calculated. This term comes from scanning probe microscopy, where each mutifrequency lockin measurement corresponds to one image pixel.

tones

The components of a multifrequency waveform, or components of a frequency comb. Tones have frequency, amplitude and phase, or alternatively, frequency and two quadrature amplitudes. Sometimes tones are loosely referred to ‘frequencies’, but strictly speaking, the frequency is only one of three attributes of a tone.

The tones in the MLA™, are specified by a tone index i = 0,1,2,\dots,N-1, where N is the number of tones in the MLA™. The frequency array maps the tone index to frequency.

programming symbols: freqs = narray * df

  • freqs : np.array(dtype=float) [Hz] frequencies of tones.

  • narray : np.array(dtype=int) [-] frequencies of tones as multiples of df.

  • df : float [Hz] measurement bandwidth

math symbols: f_i = n_i \delta f

tuning

The process of choosing the frequency of all measurement and excitation tones, as well as the measurement bandwidth, such that all have an integer relation to one base tone. In mathematical terms, tuning enforces the orthogonality of the drive tones and all their intermodulation products, on the finite interval of time over which the signal is integrated.

units

The MLA™ is a digital instrument that works with discrete numbers. We use the word ‘units’ in this context to distinguish which number we refer to:

  • PCU - phase counter units, integer between 0 and 2**42.

  • ADU - analog to digital units, integer steps of AD converter.

  • DAU - digital to analog units, integer steps of DA converter.

The documentation should give physical units in hard brackets e.g. [Hz], unless the quantity is obviously non-dimensional (i.e. unit-less), in which case one could also write [-].

waveform period

The period of a multifrequency signal, for example the period of the drive waveform or period of the response waveform.

programing symbol - T = 1/Df

math symbol T=1/\Delta f